For years, some researchers have argued that the evidence for global warming is not nearly as strong as has been officially claimed. The details of the arguments are often technical. As a result, policy makers and other people outside the debate have relied on the pronouncements of a group of climate scientists. I think that is unnecessary. I believe that what is arguably the most important reason to doubt global warming can be explained in terms that most people can understand.
Figure 1. Global temperatures.
Significance
Consider the graph of global
temperatures in Figure 1, which uses data from NASA. At first, it might
seem obvious that the graph shows an increase in temperatures. In fact,
the story is more involved, as we will now see.
Imagine tossing a coin ten times. If the coin came up Heads each time, we would have very significant evidence that the coin was not a fair coin. Suppose instead that the coin was tossed only three times. If the coin came up Heads each time, we would not have significant evidence that the coin was unfair: getting Heads three times can reasonably occur just by chance.
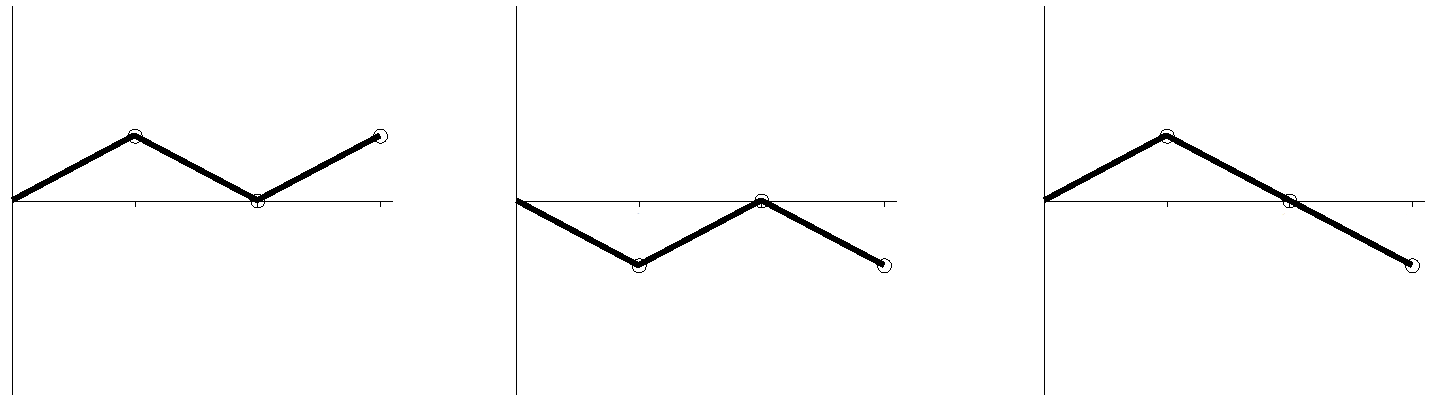Figure 2. Coin tosses: H, T, H (left); T, H, T (mid); H, T, T (right).
In Figure 2, each graph has three segments, one segment for each toss of a coin. If the coin came up Heads, then the segment slopes upward; if it came up Tails, then the segment slopes downward. In Figure 2, the graph on the left illustrates tossing Heads, Tails, Heads; the middle graph illustrates Tails, Heads, Tails; and the last graph illustrates Heads, Tails, Tails.
Figure 3. Coin tosses: H, H, H.
Now consider Figure 3. At first, it might seem obvious that the graph shows an increase. This graph, however, illustrates Heads, Heads, Heads. Three Heads is not significant evidence for anything other than random chance occurring. A statistician would say that although Figure 3 shows an increase, the increase is “not significant”.
Suppose that instead of tossing coins, we roll ordinary six-sided dice. If a die comes up 1, a line segment is drawn sloping downward; if it comes up 6, a segment is drawn sloping upward; and if it comes up 2, 3, 4, or 5, a segment is drawn straight across. We will roll each die three times. Some examples are given in Figure 4.
Figure 4. Dice rolls: 3, 6, 3 (left); 1, 5, 2 (mid); 4, 6, 1 (right).
Next consider Figure 5, which corresponds to rolling 6 three times. This outcome will occur by chance just once out of 216 times, and so it gives significant evidence that the die is not rolling randomly. That is, the increase shown in Figure 5 is significant.
Figure 5. Dice rolls: 6, 6, 6.
Note that Figure 3 and Figure 5 look identical. In Figure 3, the increase is not significant; yet in Figure 5, the increase is significant. These examples illustrate that we cannot determine whether a line shows a significant increase just by looking at it. Rather, we must know something about the process that generated the line. In practice, the process might be very complicated, which can make the determination difficult.
Consider again the graph of global temperatures in Figure 1. We cannot tell if global temperatures are significantly increasing just by looking at the graph. Moreover, the process that generates global temperatures—Earth's climate system—is extremely complicated. Hence determining whether there is a significant increase is likely to be difficult.
Time series
This brings us to the statistical concept of a time series. A time series is any series of
measurements taken at regular time intervals. Examples include the following:
prices on the New York Stock Exchange at the close of each business day; the
maximum temperature in London each day; the total wheat harvest in Canada
each year. Another example is the average global temperature each year.
In the analysis of time series, a basic question is how to determine whether a given series is significantly increasing (or decreasing). The mathematics of time-series analysis gives us some methods to answer that question. The first thing to do is to state what we know about the time series. For example, we might state that the series goes up one step whenever a certain coin comes up Heads, and that the series comprises three upward steps, as in Figure 3. The next things to do are some computations based on what we have stated. For example, we compute that the probability of a coin coming up Heads three times in a row is ½ × ½ × ½ = ⅛, i.e. a 12.5% probability of occurring randomly. From that, we conclude that the three upward steps in the coin-toss time series can be reasonably attributed to chance—and thus that the increase shown in Figure 3 is not significant.
Similarly, in order to determine if the global temperature series is significantly increasing, we must first state what we know about the temperature series. What do we know about the series? Not enough to do viable time-series analysis, unfortunately. What we must do, then, is make some assumptions about the series, and then do our analysis based on those assumptions. This is the way that is advocated by time-series analysts. As long as the assumptions are reasonable, we can be confident that the conclusions drawn from our analysis are reasonable.
The IPCC assumption
The primary body advising governments on global warming is the U.N.'s Intergovernmental Panel on Climate Change (IPCC).
The IPCC's most-recent report on the scientific basis for global warming was published in 2007.
Chapter 3 considers the global temperature series illustrated in Figure 1.
The chapter's principle conclusion is that the increase in global temperatures is
extremely significant.
To draw that conclusion, the IPCC had to make an assumption about the global temperature series. The assumption that it made is known as the “AR1” assumption (this is from the statistical concept of “first-order autoregression”). The assumption implies, among other things, that only the current value in a time series has a direct effect on the next value. For the global temperature series, it means that this year's temperature affects next year's, but temperatures in previous years do not. For example, if the last several years were extremely cold, that on its own would not affect the chance that next year will be colder than average. Hence, the assumption made by the IPCC seems intuitively implausible.
There are standard checks to (partially) test whether a time series conforms to a given statistical assumption. If a series does not conform, then any conclusions based on that assumption must be considered unfounded. For example, if the significance of the increase in Figure 5 were computed assuming that the probability of a line segment sloping upward were one in two, instead of one in six, then that would lead to an incorrect conclusion. The IPCC chapter, however, does not report doing such checks.
In other words, the assumption used by the IPCC is simply made by proclamation. Science is supposed to be based on evidence and logic. The failure of the IPCC to present any evidence or logic to support its assumption is a serious violation of basic scientific principles.
Moreover, standard checks show that the global temperature series does not conform to the assumption made by the IPCC; one such check is discussed in a separate section below. Thus, the claim that the increase in global temperatures is significant—the principal conclusion of a major chapter of the IPCC report—was based on an assumption that is insupportable. More generally, the IPCC has failed to demonstrate that global temperatures are significantly increasing.
These problems are not unique to the IPCC, either. The U.S. Climate Change Science Program (CCSP), which advises Congress, published its report on temperature changes in 2006. That report relies on the same insupportable assumption as the IPCC chapter.
None of this is opinion. This is factual and indisputable. And it applies to any warming—whether attributable to humans or to nature. Until research to choose an appropriate assumption is done, no conclusion about the significance of temperature changes can be drawn.
Mr. Keenan previously did mathematical research and financial trading on Wall Street and in the City of London; since 1995, he has been studying independently. He supports environmentalism and energy security.
An insupportable assumption
Figure 6. Sunlight intensity (inverted) and global ice volume.
Changes
Over many millennia, the most important fluctuations in Earth's climate have been
those related to the ice ages.
The ice ages are caused by natural variations in Earth's orbit around the sun.
Those variations in the orbit alter the intensity of summertime sunlight. Some
relevant data is presented in Figure 6: the black line represents the amount
of ice globally and the green line represents the intensity of
summertime sunlight in the Northern Hemisphere (where the effects are
greatest). Notice, though, that the similarity between the two lines is very weak.
Figure 7. Sunlight intensity (inverted) and changes in global ice volume.
Why is the similarity so weak? To understand what is happening, we have to consider the changes in the amount of ice globally. For example, if the amount of ice at different times were 17, 15, 14, 19, …, then subtracting adjacent amounts gives the changes: 2, 1, −5, …. The black line in Figure 7 shows the changes in the amount of ice, while the green line, as before, shows the intensity of summertime sunlight. Now the similarity between the two lines is strong. This is excellent evidence that the ice ages are indeed caused by orbital variations. (There is other evidence as well.)
A connection between ice ages and orbital variations was first proposed in 1920, by the Serbian astrophysicist Milutin Milankovitch. To check the proposed connection, data on the amount of ice in past millennia is obviously needed; such data became available in 1976. Yet it was not until 2006 that scientists considered the changes in the amount of ice. In other words, it took 30 years for scientists to think to do the subtraction needed to draw the black line in Figure 7. During those three decades, scientists analyzing Milankovitch's proposal based their studies on graphs like Figure 6, and they considered a variety of ideas to try to explain the weak similarity between the two lines.
Alternative assumptions
The foregoing raises a question:
for global temperatures, what happens if we analyze the changes, instead of the
temperatures themselves? It turns out that then there is an obvious alternative to
the assumption used by the IPCC. How good is the alternative assumption compared
to the IPCC assumption?
One common method of comparing assumptions is to use what statisticians call “AICc”
(Akaike Information Criterion with correction). This method shows that the alternative is
so much better than the IPCC assumption, that we conclude the IPCC assumption is insupportable.
That is, the IPCC made the same mistake as the scientists who worked for 30 years to
verify Milankovitch's proposal: failing to consider the changes in a series.
Under the alternative assumption, the increase in global temperatures is not significant. We do not know, however, whether the alternative assumption itself is reasonable—other assumptions might be even better. Determining how viable the alternative assumption is would require study. There have been studies that consider other assumptions and thereby reach different conclusions about the temperature data. The IPCC report nods toward such studies, but without acknowledging that the soundness of its conclusions rests upon its choice of assumption—or that making a good choice, one that well corresponds with physical reality, requires further, difficult research.
Technical details for this essay are at www.informath.org/media/a41/b8.pdf.